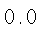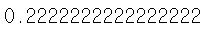이상치란?
변수 범위에서 많이 벗어난 아주 작은 값이나 아주 큰 값으로, 일반화된 모델을 생성하는데 악영향을 끼치는 값으로 이상치를 포함하는 레코드를 제거하는 방법으로 이상치를 제거한다.
이상치는 결측치와 다르게 값을 추정을 하는 것이 아니라 제거해야한다.(절대 추정의 대상이 아님에 주의한다.)
이상치를 제거해야하는 대표적인 모델들은 클래스의 평균을 쓰는 모델들이다.(트리계열 모델, 거리를 사용하는 모델:KNN, 회귀모델(회귀모델도 학습될 때 미분 하는 과정에서 평균을 사용)) →이런 모델들은 이상치를 제거해야만 일반화된 모델을 만들수 있다.

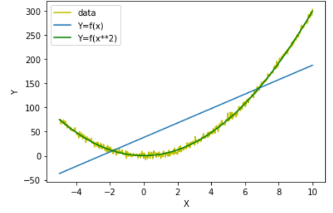
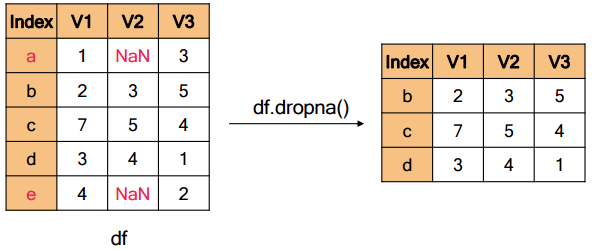
위의 그림에서 총 7개의 레코드가 있다. 빨간색 레코드는 다른 레코드에 비해서 많이 벗어나있다.
회귀 모델을 만들었는데 빨간색 레코드의 영향을 받아서 일반적인 다른 레코드를 설명하지 못하고 위쪽으로 쏠렸다.
빨간색 레코드인 이상치를 제거한 다음에 모델을 만들면 일반화된 모델이 만들어질 것이다.
이상치 판단 방법 1. IQR 규칙 활용
변수별로 IQR 규칙을 만족하지 않는 샘플들을 판단하여 삭제하는 방법이다.
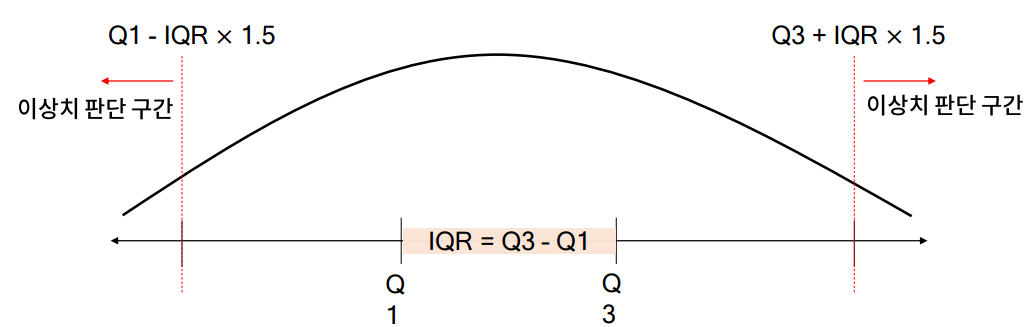
직관적이고 사용이 간편하다는 장점이 있지만, 단일 변수로 이상치를 판단하기 어려운 경우가 있다는 문제가 있다.
즉, 단일 변수로 보면 이상치이지만 여러개의 변수로 같이 보면 이상치가 아니거나, 단일 변수로 보면 이상치가 아니지만 여러개의 변수로 같이 보면 이상치인 경우가 있다는 말이다. 이럴 경우 IQR을 사용하게 되면 완벽히 무시되는 단점이 있다.
결론: IQR 기준만 가지고 이상치라고 단언할 수는 없다.
(TIP) IQR rule이라는 것은 boxplot을 그릴 때 점으로 표시된 것들이 IQR rule에 의한 이상치이다.
- 관련 문법: numpy.quantile
array의 q번째 quantile(분위수)을 구하는 함수이다.
-주요 입력
▷a: input array(list, ndarray등)
▷q: quantile(0과 1사이)
## 코드 실습 ##
import os
os.chdir(r"C:\Users\82102\Desktop\데이터전처리\머신러닝 모델의 성능 향상을 위한 전처리\5. 머신러닝 모델의 성능 향상을 위한 전처리\데이터")
import pandas as pddf = pd.read_csv("glass.csv")
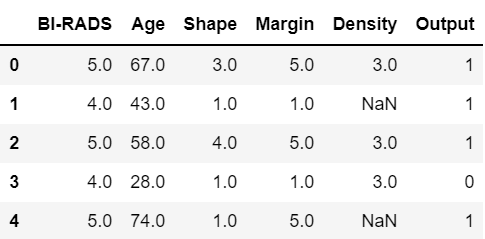
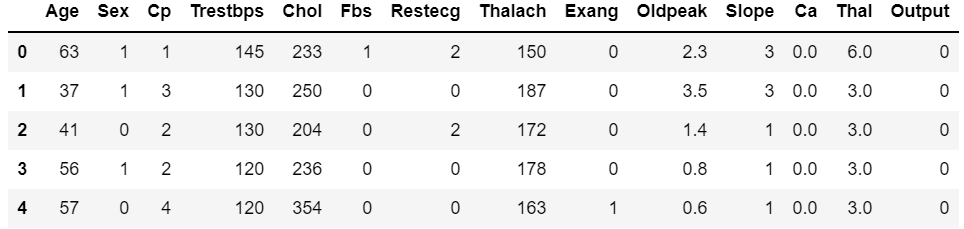
df.head()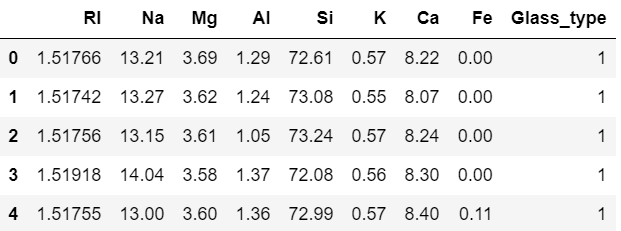
# 특징과 라벨 분리
X = df.drop('Glass_type', axis=1)
Y = df['Glass_type']# 학습 데이터와 평가 데이터 분리
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, Y)
x_train.shape
x_train1 = x_train.copy() # 이상치 비율을 조정할수도 있으니 복사본 생성import numpy as np
def IQR_rule(val_list): # 한 특징에 포함된 값(열 벡터)
# IQR 계산
Q1 = np.quantile(val_list, 0.25) # 제 1사분위수(25%)
Q3 = np.quantile(val_list, 0.75) # 제 3사분위수(75%)
IQR = Q3-Q1
# IQR rule을 위배하지 않는 bool list 계산(True: 이상치 x, False: 이상치 0)
not_outlier_condition = (Q3 + 1.5 * IQR > val_list) & (Q1 - 1.5 * IQR < val_list)
return not_outlier_condition# apply를 이용하여 모든 컬럼에 IQR rule 함수 적용
conditions = x_train.apply(IQR_rule)
conditions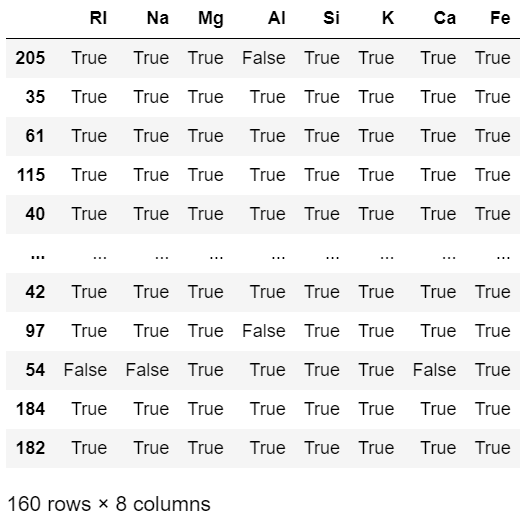
# 하나라도 IQR 규칙을 위반하는 요소를 갖는 레코드를 제거하기 위한 규칙
total_condition = conditions.sum(axis=1) == len(x_train.columns)
x_train = x_train.loc[total_condition] # 이상치 제거
x_train
x_train.shape # 45개 삭제됨
이상치 비율이 45 / 160 = 0.28125로 약 30프로이다.
그렇다면 이상치가 30프로라는게 일반적인 수치라고 볼 수 있을까?
전체 데이터에서 이상치가 30프로라는 것은 사실 말이 안된다. 그래서 이 수치는 이상치 비율이라고 보기에는 매우 높다.
정답은 없지만 일반적으로 이상치의 비율은 1프로 미만이다.
위에서 (Q3 + 1.5 * IQR > val_list) & (Q1 - 1.5 * IQR < val_list)로 IQR_rule을 계산했는데 1.5는 절대적인 수치가 아니므로 이를 조절해도 무방하다. 이 수치를 크게 둘수록 이상치의 비율이 떨어진다.
그래서 이상치의 비율이 1프로 미만이 되도록 조정하는 것이 더 바람직하다.
def IQR_rule(val_list): # 한 특징에 포함된 값(열 벡터)
# IQR 계산
Q1 = np.quantile(val_list, 0.25) # 제 1사분위수(25%)
Q3 = np.quantile(val_list, 0.75) # 제 3사분위수(75%)
IQR = Q3-Q1
# IQR rule을 위배하지 않는 bool list 계산(True: 이상치 x, False: 이상치 0)
not_outlier_condition = (Q3 + 6 * IQR > val_list) & (Q1 - 6 * IQR < val_list)
return not_outlier_condition# apply를 이용하여 모든 컬럼에 IQR rule 함수 적용
conditions = x_train1.apply(IQR_rule) # axis=0
conditions# 하나라도 IQR 규칙을 위반하는 요소를 갖는 레코드를 제거하기 위한 규칙
total_condition = conditions.sum(axis=1) == len(x_train1.columns)
x_train1 = x_train1.loc[total_condition] # 이상치 제거
x_train1x_train1.shape # 3개 삭제됨
이상치의 비율이 약 1프로이다.(3 / 160)
이상치 판단 방법 2. 밀도 기반 군집화 활용
밀도 기반 군집화 기법은 군집에 속하지 않은 샘플을 이상치라고 간주하므로, 밀도 기반 군집화 결과를 활용하여 이상치를 판단할 수 있다. 이 방법의 대표적인 알고리즘이 DBSCAN이다.

이 방법은 단일 변수로 이상치를 판단하는 IQR_rule과 다르게,
다른 특징과의 관계까지 반영할 수 있다는 장점이 있다. 하지만 DBSCAN 등의 밀도 기반 군집화 모델은 파라미터 튜닝이 쉽지 않다는 단점이 있다.(DBSCAN으로 모델을 만들 때 eps, min_samples와 같은 파라미터 튜닝이 어렵다.)
- 관련 문법: sklearn.cluster.DBSCAN
DBSCAN 군집화를 수행하는 인스턴스를 생성하는 함수이다.
-주요 입력
▷eps(앱실론): 이웃이라 판단하는 반경
▷min_samples: 중심점이라 판단하기 위해, eps 내에 들어와야 하는 최소 샘플 수
▷metric: 사용하는 거리 척도
-주요 attribute
▷.labels_: 각 샘플이 속한 군집 정보(-1이면 이상치)
## 코드 실습 ##
import os
os.chdir(r"C:\Users\82102\Desktop\데이터전처리\머신러닝 모델의 성능 향상을 위한 전처리\5. 머신러닝 모델의 성능 향상을 위한 전처리\데이터")
import pandas as pd
import numpy as npdf = pd.read_csv("glass.csv")
df.head()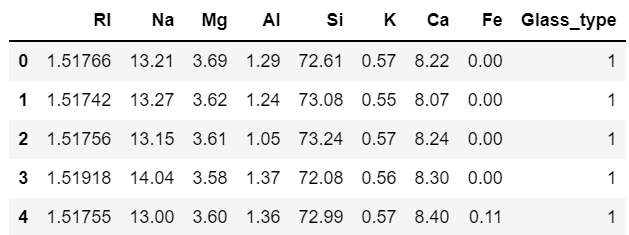
# 특징과 라벨 분리
X = df.drop('Glass_type', axis=1)
Y = df['Glass_type']# 학습 데이터와 평가 데이터 분리
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, Y)
x_train.shape
from scipy.spatial.distance import cdist
from sklearn.cluster import DBSCAN
cdist를 불러온 이유는 DBSCAN의 파라미터를 조정할 때 참고하기 위해서 불러왔다. 앱실론이라는 것은 결국 거리일텐데 그 거리가 데이터의 스케일마다 차이가 크기 때문에 거리를 미리 판단하기 쉽지 않아서 참고하고자 cdist를 불러왔다.
즉, cdist를 이용하면 쉽게 데이터간에 거리를 구할 수 있다.
# x_train과 x_train 거리 행렬계산 => DBSCAN의 파라미터를 설정하기 위함
DM = cdist(x_train, x_train)
DM
np.quantile(DM, 0.1)
# 샘플 간 거리의 10% quantile이 0.6455정도임을 확인
여기서 10%는 작은값을 기준으로 상위 10%를 말하는 것이다. 즉, 작은값을 기준으로 상위 10%의 거리가 0.6455정도 라는 것이다. 0.6455라고 나온값은 단순히 참고하는 수치이고 이게 정확한 기준은 아니다.
np.mean(DM), np.min(DM)처럼 평균이나 최솟값을 쓰기에는 대각행렬은 같은 레코드끼리 거리기 때문에 전부 0이고 대각 행렬 기준 대칭으로 값이 같기 때문에 평균이나 최솟값을 쓰기 어렵다. 그래서 분포통계량인 quantile을 사용했다.
cluster_model = DBSCAN(eps=0.6455, min_samples=3).fit(x_train)
print(sum(cluster_model.labels_ == -1))
# 33개가 이상치로 판단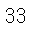
33개가 이상치로 판단됐다. 이 정도면 너무 많은 양의 이상치라고 판단되어서 파라미터 조정을 하기로 결정했다.
cluster_model = DBSCAN(eps=2, min_samples=3).fit(x_train) # eps=2로 파라미터 조정
print(sum(cluster_model.labels_ == -1))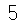
앱실론을 크게 늘리면 당연히 반경내에 샘플이 많이 들어갈 가능성이 높다. 그래서 이상치라고 판단되는 데이터의 수도 줄어들 것이다.
결과 5 / 160으로 이상치 비율이 약 3프로로 일반적인 이상치 비율인 1프로 미만보다 많은 수치이긴 하지만 이 정도면 괜찮겠다라고 판단했다. 즉, 5개 정도면 괜찮은 양이라고 판단하여 삭제를 한다.
x_train = x_train[cluster_model.labels_ != -1]
x_train.shape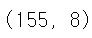
=>학습 데이터에서 이상치를 제거해서 일반화된 모델을 만든 후 평가 데이터로 모델 성능 평가
'데이터 전처리 > 머신러닝 모델의 성능 향상을 위한 전처리' 카테고리의 다른 글
| 클래스 불균형 문제 (0) | 2022.12.27 |
|---|---|
| 변수 분포 문제-특징간 스케일 차이 해결하기(스케일링) (0) | 2022.12.26 |
| 변수 분포 문제-변수 치우침 제거 (0) | 2022.12.26 |
| 변수 분포 문제-특징 간 상관성 제거(특징 선택) (0) | 2022.12.25 |
| 변수 분포 문제-특징과 라벨 간 약한 관계 또는 비선형 관계일때 (0) | 2022.12.22 |