1. 물리적 지표면(Earth surface): 산, 건물 등과 같이 구성된 복잡한 지구를 수학적으로 해석하기 어려움
→ 우리가 살고 있는 지구 그 자체
수학적 해석 x
2. 지오이드(Geoid): 등포텐셜면(포텐셜이 일정한 면을 쭉 이어준 것)
→ 중력이 일정한 면을 쭉 이어서 동그랗게 만들어 진 면
지구의 형상을 중력으로 표현한 것
지오이드도 크고 작음에 따라서 굉장히 울퉁불퉁하고 이 것을 가지고 지표면의 위치를 정의하기에는 무리가 있음
그래서 나온 것이 '기준 타원체'라는 개념
3. 기준 타원체(Reference Ellipsoid): 지오이드와 가장 유사하게 수학적으로 정의된 타원체
→ 장반경(긴 반지름) a, 단반경(짧은 반지름) b가 정의되면 기준 타원체를 정의할 수 있음→ a와 b가 정의되면 편평도 f, 이심률 e² 라는 값을 계산할 수 있음
- 편평도는 우리가 만든 기준 타원체가 얼마나 편평한가, 즉 얼마나 구에서 멀어진 모양인가를 나타냄(구에 가까울수록 ∞에 가까워짐)
- 이심률은 기준 타원체가 얼마나 찌그러져 있는가를 나타냄(이심률이 클수록 많이 찌그러진 타원체)
- 편평도 f = (a-b) / a
- 이심률 e² = 2f- f²
앞 장에서 설명했듯이, 기준 타원체는 국지적 기준 타원체(local) / 범지구적 기준 타원체(global)로 나눌수 있음
- 국지적 기준 타원체: 지역적, 특정 부분에 잘 맞는 타원체 (ex: Bessel타원체)
- 범지구적 기준 타원체: 전지구에 잘 맞는 타원체 (ex: GRS80타원체, WGS84타원체)
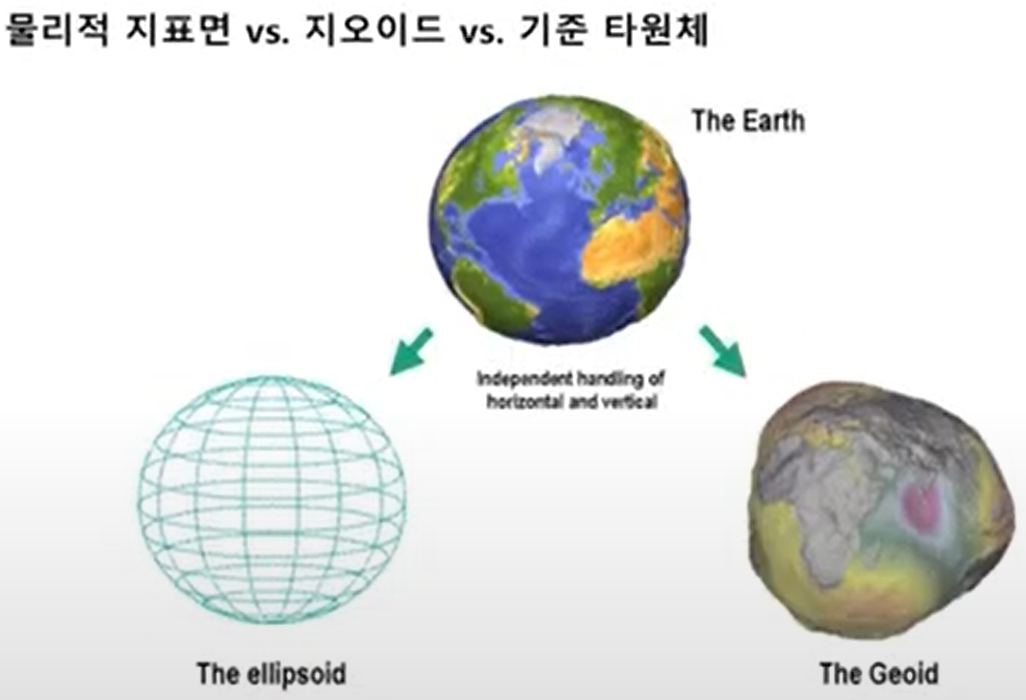
지구의 형상을 표현하기 위해서 물리적 지표면, 지오이드 만으로는 수학적으로 표현하기 어렵기 때문에 나온 개념이 '기준 타원체'
기준 타원체가 지오이드랑 얼마나 잘 맞게 만들어지는지를 표현하는 개념이 "연직선 편차"라는 개념
→ 지오이드에서 내린 수직선과 기준 타원체에서 내린 수직선이 이루는 각
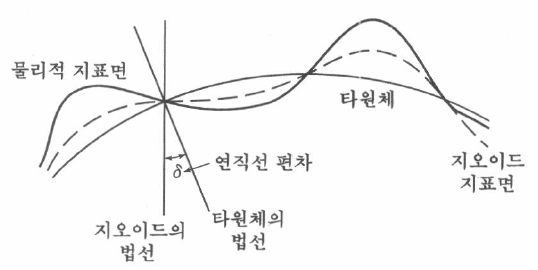
기준 타원체가 실제 지오이드에 맞게 잘 정의가 되어있다면 해당 위치에서 연직선 편차는 작음
즉, 어떤 지역에서 연직선 편차가 작다는 것은 해당 지역에 기준 타원체가 지오이드에 맞게 잘 정의가 된 것으로 판단