지도학습
1. 분류
결정값이 카테고리 값(이산값)
2. 회귀
결정값이 숫자값(연속값)
회귀 개요
회귀분석은 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법이다. 통계학 용어를 빌리자면 회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다.
예를 들어 아파트의 방 개수, 방 크기, 주변 학군 등 여러 개의 독립변수에 따라 아파트 가격이라는 종속변수가 어떤 관계를 나타내는지 모델링하고 예측하는 것
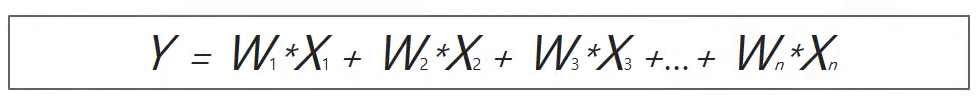
Y: 종속변수
X1, X2, ..., Xn: 독립변수
W1, W2, ..., Wn: 각 독립변수의 값에 영향을 미치는 회귀계수(Regression coefficients)
머신러닝 관점에서 독립변수는 피처에 해당되며, 종속변수는 결정값에 해당된다.
따라서 머신러닝 회귀 예측의 핵심은 '주어진 피처와 결정값 데이터 기반에서 학습을 통해 최적의 회귀계수를 찾아내는 것'
회귀의 유형
회귀는 회귀계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러 가지 유형으로 나눌 수 있다.
1. 선형/비선형
회귀계수가 선형이면 선형 회귀 / 회귀계수가 비선형이면 비선형 회귀
2. 독립변수의 개수
독립변수 개수가 1개이면 단일 회귀 / 독립변수 개수가 여러개이면 다중 회귀
3. 종속변수의 개수
종속변수 개수가 1개이면 단변량 회귀 / 종속변수 개수가 여러개이면 다변량 회귀
선형 회귀의 종류
여러 가지 회귀 중에서 선형 회귀가 가장 많이 사용된다. 선형 회귀는 실제값과 예측값의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식
선형 회귀 모델은 규제(Regularization) 방법에 따라 다시 별도의 유형으로 나뉠 수 있다. 여기서 규제는 일반적인 선형 회귀의 과적합 문제를 해결하기 위해서 회귀계수에 패널티 값을 적용하는 것이다.
● 일반 선형 회귀
예측값과 실제값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀계수를 최적화하며, 규제(Regularization)를 적용하지 않은 모델
● 릿지(Ridge) 회귀
릿지 회귀는 선형 회귀에 L2 규제를 적용한 회귀 모델
L2 규제는 상대적으로 큰 회귀계수 값의 예측 영향도를 감소시키기 위해서 회귀계수 값을 더 작게 만드는 규제
● 라쏘(Lasso) 회귀
라쏘 회귀는 선형 회귀에 L1 규제를 적용한 회귀 모델
L1 규제는 예측 영향력이 작은 피처의 회귀계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것 → 이러한 특성으로 L1 규제는 피처 선택 기능으로도 불림
● 엘라스틱넷(ElasticNet) 회귀
L2, L1 규제를 함께 결합한 모델
주로 피처가 많은 데이터 세트에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 회귀계수 값의 크기를 조정
● 로지스틱(Logistic) 회귀
로지스틱 회귀는 회귀라는 이름이 붙어 있지만, 사실은 분류에 사용되는 선형 모델 → 로지스틱 회귀는 매우 강력한 분류 알고리즘
이진 분류뿐만 아니라 희소 영역의 분류(예를 들어 텍스트 분류)에서 뛰어난 예측 성능을 보임 → 이진 분류에 아주 효과적
'파이썬 머신러닝 완벽가이드 > [5장] 회귀' 카테고리의 다른 글
| 다항회귀(Polynomial Regression) (0) | 2023.04.10 |
|---|---|
| LinearRegression을 이용해 보스턴 주택 가격 예측 (0) | 2023.03.20 |
| LinearRegression, 회귀 평가 지표 (0) | 2023.03.19 |
| 경사 하강법(Gradient Descent) (0) | 2023.03.10 |
| 단순 선형 회귀를 통한 회귀 이해 (0) | 2023.03.08 |