●분류와 회귀를 둘 다 지원한다.(분류-DecisionTreeClassifier / 회귀-DecisionTreeRegressor)
●결정 트리는 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리(Tree) 기반의 분류 규칙을 만드는 것이다.(If-Else 기반 규칙)
→쉽게 생각하면 스무고개 게임과 유사하다.
●따라서 데이터의 어떤 기준을 바탕으로 규칙을 만들어야 가장 효율적인 분류가 될 것인가가 알고리즘의 성능을 크게 좌우한다.

규칙 노드로 표시된 노드는 규칙 조건이 되는 것이고, 리프 노드로 표시된 노드는 결정된 클래스 값이다. 그리고 새로운 규칙 조건마다 서브 트리가 생성된다.
데이터 세트에 피처가 있고 이러한 피처가 결합해 규칙 조건을 만들 때마다 규칙 노드가 만들어진다. 하지만 많은 규칙이 있다는 것은 곧 분류를 결정하는 방식이 더욱 복잡해진다는 얘기이고, 이는 곧 과적합으로 이어지기 쉽다.
즉, 트리의 깊이(depth)가 깊어질수록 결정 트리의 예측 성능이 저하될 가능성이 높다.
그래서 가능한 한 적은 결정 노드로 높은 예측 정확도를 가지려면 데이터를 분류할 때 최대한 많은 데이터 세트가 해당 분류에 속할 수 있도록 결정 노드의 규칙이 정해져야 한다. 이를 위해 어떻게 트리를 분할(split)할 것인가가 중요한데 최대한 균일한 데이터 세트를 구성할 수 있도록 분할하는 것이 필요하다.
균일한 데이터 세트가 어떤 것을 의미하는지 살펴보자.

C의 경우 모두 검은 공으로 구성되므로 데이터가 모두 균일하다. B의 경우 일부 하얀 공을 가지고 있지만, 대부분 검은 공으로 구성되어 다음으로 균일도가 높다. A의 경우는 검은 공 못지않게 많은 하얀 공을 가지고 있어 균일도가 제일 낮다.
이러한 데이터 세트의 균일도는 데이터를 구분하는 데 필요한 정보의 양에 영향을 미친다.
예를 들어, 눈을 가린 채 데이터 세트 C에서 하나의 데이터를 뽑았을 때 데이터에 대한 별다른 정보 없이도 '검은 공'이라고 쉽게 예측할 수 있지만 A의 경우는 상대적으로 균일도가 낮기 때문에 같은 조건에서 데이터를 판단하는데 있어 더 많은 정보가 필요하다.
이렇듯 결정 노드는 정보 균일도가 높은 데이터 세트를 먼저 선택할 수 있도록 규칙 조건을 만든다. 즉, 정보 균일도가 높은 데이터 세트로 쪼개질 수 있도록 조건을 찾아 서브 데이터 세트로 만들고, 다시 이 서브 데이터 세트에서 균일도가 높은 자식 데이터 세트로 쪼개는 방식을 반복하는 방식으로 데이터 값을 예측하게 된다.
(예를 들어 박스 안에 30개의 레고 블록이 있는데, 각 레고 블록은 '형태' 속성으로 동그라미, 네모, 세모, '색깔' 속성으로 노랑, 빨강, 파랑이 있다. 이 중 노랑색 블록의 경우 모두 동그라미로 구성되고 , 빨강과 파랑 블록의 경우는 동그라미, 네모, 세모가 골고루 섞여 있다고 한다면 각 레고 블록을 형태와 색깔 속성으로 분류하고자 할 때 가장 첫 번째로 만들어져야 하는 규칙 조건은 if 색깔 == '노랑색'이 된다. 왜냐하면 노란색 블록이면 모두 노란 동그라미 블록으로 가장 쉽게 예측할 수 있고, 그다음 나머지 블록에 대해 다시 균일도 조건을 찾아 분류하는 것이 가장 효율적인 분류 방식이기 때문이다.)
이러한 정보 균일도를 측정하는 방법은 정보 이득, 지니계수가 있다.
<정보 균일도 측정 방법>
1) 정보 이득(Information Gain)
정보 이득은 엔트로피 개념을 기반으로 한다. 엔트로피는 주어진 데이터 집합의 혼잡도를 의미하는데, 서로 다른 값이 섞여 있으면 엔트로피가 높고, 같은 값이 섞여 있으면 엔트로피가 낮다.
정보 이득 지수는 1에서 엔트로피 지수를 뺀 값으로 '1-엔트로피 지수'이다. 결정 트리는 이 정보 이득 지수로 분할 기준을 정하는데 정보 이득이 높은 속성을 기준으로 분할한다.
(정보 균일도가 높은 데이터 세트로 쪼개질 수 있도록→정보 이득이 높은 속성→엔트로피 낮음→같은 값이 섞여 있음)
2) 지니 계수
지니 계수는 원래 경제학에서 불평등 지수를 나타낼 때 사용하는 계수이다. 0이 가장 평등하고 1로 갈수록 불평등하다.
머신러닝에 적용될 때는 지니 계수가 낮을수록 데이터 균일도가 높은 것으로 해석해 지니계수가 낮은 속성을 기준으로 분할한다.
(정보 균일도가 높은 데이터 세트로 쪼개질 수 있도록→지니계수가 낮은 속성→평등→같은 값이 섞여 있음)
⇛ 결정 트리 알고리즘을 사이킷런에서 구현한 DecisionTreeClassifier는 기본으로 지니 계수를 이용해 데이터 세트를 분할한다. 결정 트리의 일반적인 알고리즘은 데이터 세트를 분할하는 데 가장 좋은 조건, 즉 정보 이득이 높거나 지니계수가 낮은 조건을 찾아서 자식 트리 노드에 걸쳐 반복적으로 분할한 뒤, 데이터가 모두 특정 분류에 속하게 되면 분할을 멈추고 분류를 결정한다.
<결정 트리의 특징>
1) 장점
- 정보의 '균일도'라는 룰을 기반으로 하고 있어서 쉽고 직관적이며 시각화로 표현까지 할 수 있음
- 정보의 '균일도'만 신경쓰면 되므로 특별한 경우를 제외하고는 피처의 스케일링이나 정규화 등의 전처리 작업이 필요 없다.
2) 단점
- 과적합으로 알고리즘 성능이 떨어진다. 이를 극복하기 위해 트리의 크기를 사전에 제한하는 튜닝이 필요함
위의 단점을 설명하자면
피처 정보의 균일도에 따른 룰 규칙으로 서브 트리를 계속 만들다 보면 피처가 많고 균일도가 다양하게 존재할수록 트리의 깊이가 커지고 복잡해질 수 밖에 없다. 결과적으로 복잡한 학습 모델에 이르게 된다. 복잡한 학습 모델은 결국에는 실제 상황에(테스트 데이터 세트) 유연하게 대처할 수 없어서 예측 성능이 떨어질 수밖에 없다.
<Graphviz를 이용한 결정 트리 모델의 시각화>
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
# DecisionTreeClassifier 생성
dt_clf = DecisionTreeClassifier(random_state=156)
# 붓꽃 데이터를 로딩하고, 학습과 테스트 데이터 세트로 분리
iris_data = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target,
test_size=0.2, random_state=11)
# DecisionTreeClassifier 학습
dt_clf.fit(X_train, y_train)from sklearn.tree import export_graphviz
# export_graphviz()의 호출 결과로 out_file로 지정된 tree.dot 파일을 생성함
export_graphviz(dt_clf, out_file='tree.dot',class_names=iris_data.target_names,
feature_names=iris_data.feature_names, impurity=True, filled=True)import graphviz
# 위에서 생성된 tree.dot 파일을 Graphviz가 읽어서 주피터 노트북상에서 시각화
with open("tree.dot") as f:
dot_graph = f.read()
graphviz.Source(dot_graph)
시각화된 결정 트리의 맨 윗부분에서 몇 단계 아래로 내려가 보면서 어떻게 트리가 구성되는지 구체적으로 보겠다.

●petal_length(cm) <= 2.45 와 같이 피처의 조건이 있는 것은 자식 노드를 만들기 위한 규칙 조건이다. 이 조건이 없으면 리프 노드이다.
●gini는 value=[ ]로 주어진 데이터 분포에서의 지니 계수이다.
●samples는 현 규칙에 해당하는 데이터 건수이다.
●value=[ ]는 클래스 값 기반의 데이터 건수이다. 붓꽃 데이터 세트는 클래스 값으로 0, 1, 2를 가지고 있으며, 0:Setosa, 1:Versicolr, 2:Virginica 품종을 가리킨다. 만일 value=[41, 40, 39]라면 클래스 값의 순서로 Setosa 41개, Versicolor 40개, Virginica 39개로 데이터가 구성돼 있다는 의미이다.
●class는 value 리스트내에 가장 많은 건수를 가진 결정값이다.
초록색 노드를 다시 살펴보면 38개의 샘플 데이터 중 Virginica가 단 1개이고, 37개가 Versicolor이지만 Versicolor와 Virginica를 구분하기 위해서 다시 자식 노드를 생성한다. 이처럼 결정 트리는 규칙 생성 로직을 미리 제어하지 않으면 완벽하게 클래스 값을 규별해내기 위해 트리 노드를 계속해서 만들어 간다. 이로 인해 결국 매우 복잡한 규칙 트리가 만들어져 모델이 쉽게 과적합되는 문제점을 가지게 된다.
결정 트리는 이러한 이유로 과적합이 상당히 높은 ML 알고리즘이다. 이 때문에 결정 트리 알고리즘을 제어하는 대부분 하이퍼 파라미터는 복잡한 트리가 생성되는 것을 막기 위한 용도이다.
<결정 트리 파라미터>
max_depth
- 트리의 최대 깊이를 규정
- 디폴트는 None. None으로 설정하면 완벽하게 클래스 결정값이 될 때까지 깊이를 계속 키우며 분할하거나, 노드가 가지는 데이터 개수가 min_samples_split보다 작아질 때까지 계속 깊이를 증가시킴
- 깊이가 깊어지면 min_samples_split 설정대로 최대 분할하여 과적합할 수 있으므로 적절한 값으로 제어 필요
min_samples_split
- 노드를 분할하기 위한 최소한의 샘플 데이터 수로 과적합을 제어하는데 사용됨
- 디폴트는 2이고 작게 설정할수록 분할되는 노드가 많아져서 과적합 가능성 증가
min_samples_leaf
- 분할될 경우 왼쪽과 오른쪽 자식 노드 각각이 가져야 할 최소한의 샘플 데이터 수(즉 어떤 노드가 분할할 경우, 왼쪽과 오른쪽 자식 노드 중에 하나라도 min_samples_leaf로 지정된 최소한의 샘플 데이터 수보다 더 작은 샘플 데이터 수를 갖게 된다면, 해당 노드는 더 이상 분할하지 않고 리프 노드가 된다.)
- 디폴트는 1. 큰 값으로 설정될수록, 분할될 경우 왼쪽과 오른쪽의 자식 노드에서 가져야할 최소한의 샘플 데이터 수 조건을 만족시키기 어려우므로 노드 분할을 상대적으로 덜 수행함
- min_samples_split과 유사하게 과적합 제어 용도→둘 다 큰 값으로 설정할수록 과적합 가능성 감소
max_features
- 최적의 분할을 위해 고려할 최대 피처 개수. 디폴트는 None으로 데이터 세트의 모든 피처를 사용해 분할 수행
- int형으로 지정하면 대상 피처의 개수, float형으로 지정하면 전체 피처 중 대상 피처의 퍼센트임
- 'sqrt'는 sqrt(전체 피처 개수) 선정
- 'auto'로 지정하면 sqrt와 동일
- 'log'는 log2(전체 피처 개수) 선정
- 'None'은 전체 피처 선정
max_leaf_nodes
- 말단 노드(리프 노드)의 최대 개수
이제부터 결정 트리의 하이퍼 파라미터 변경에 따른 트리 변화를 보겠다.
⊙max_depth 하이퍼 파라미터 변경에 따른 트리 변화
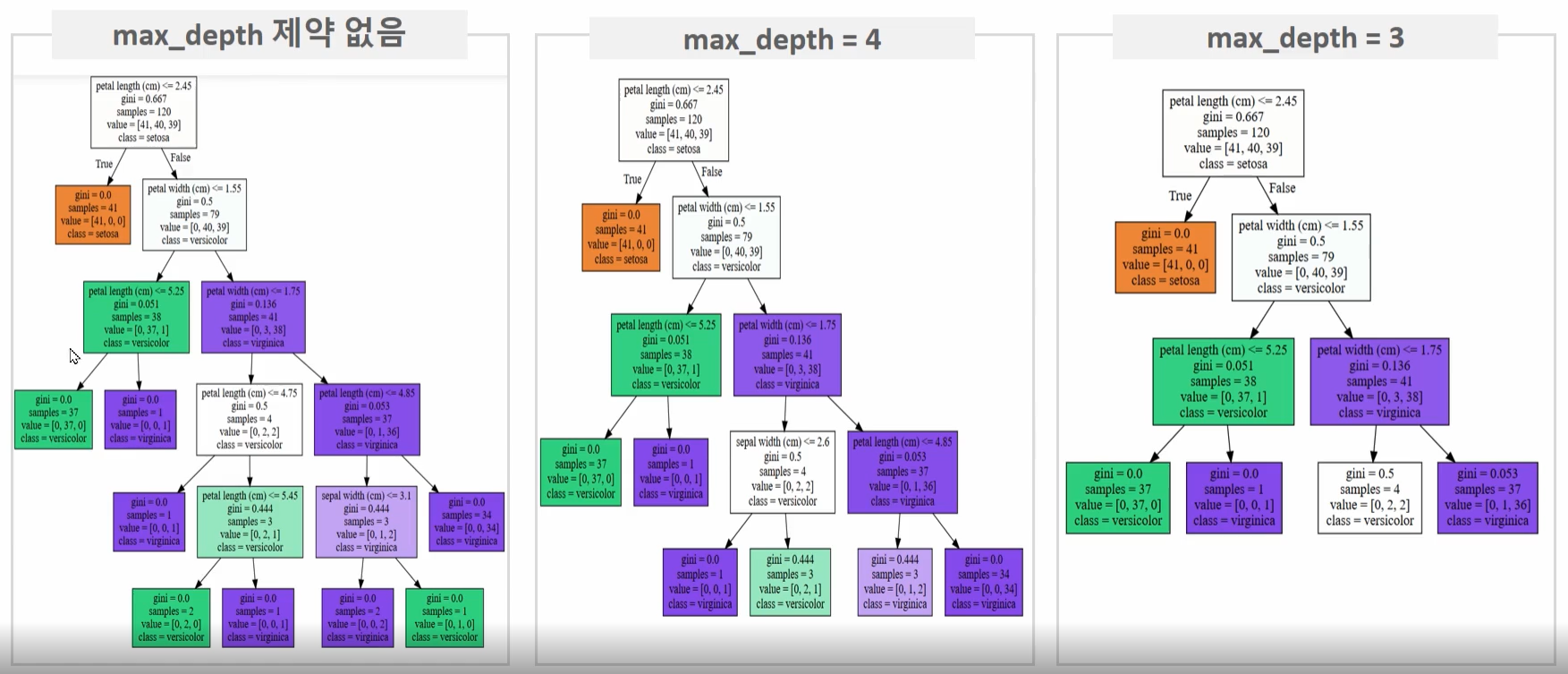
max_depth를 제한 없음에서 3개로 설정하면 트리 깊이가 설정된 max_depth에 따라 줄어들면서 더 간단한 결정 트리가 된다.
⊙min_samples_split 하이퍼 파라미터 변경에 따른 트리 변화

min_samples_split=4로 설정한 경우
맨 아래 리프 노드 중 사선 박스로 표시된 노드를 보면 샘플이 3개인데, 이 노드 안에 value가 [0, 2, 1]과 [0, 1, 2]로 서로 상이한 클래스 값이 있어도 더 이상 분할하지 않고 리프 노드가 되었다.
즉 노드를 분할하기 위한 최소한의 샘플 데이터 수가 4개는 필요한데, 3개밖에 없으므로 더 이상 분할을 하지 않고 리프 노드가 됨을 알 수 있음
→자연스럽게 트리 깊이도 줄었고 더욱 간결한 결정 트리가 만들어졌다.
⊙min_samples_leaf 하이퍼 파라미터 변경에 따른 트리 변화
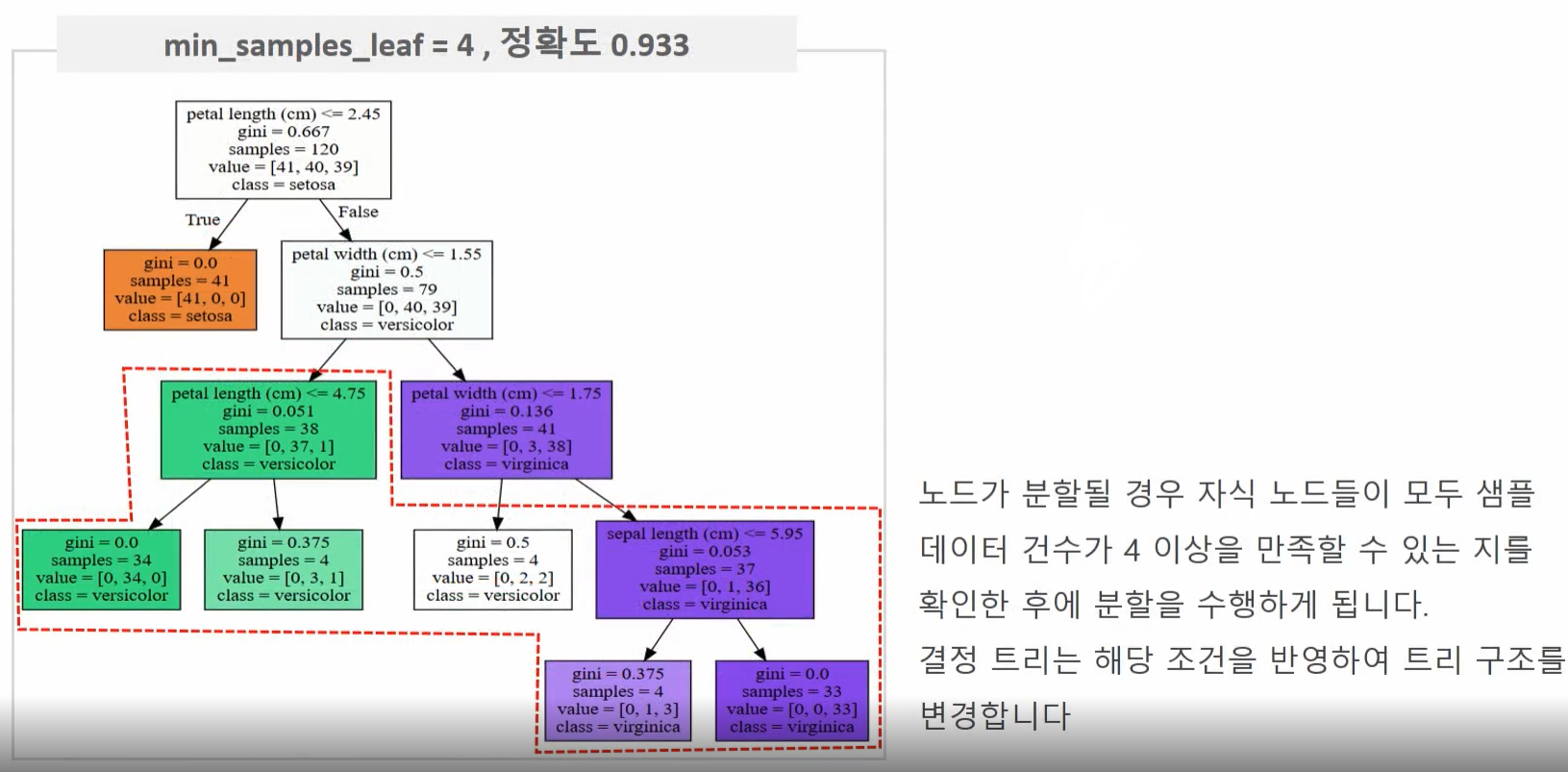
min_samples_leaf=4로 설정한 경우 노드가 분할할 때 왼쪽, 오른쪽 자식 노드가 모두 샘플 데이터 수 4 이상을 가진 노드가 되어야 하므로 디폴트인 1로 설정하는 것보다는 조건을 만족하기 어려워서 상대적으로 적은 횟수로 분할을 수행한다.
→자연스럽게 트리 깊이도 줄었고 더욱 간결한 결정 트리가 만들어졌다.
<피처의 중요 역할 지표: feature_importances_>
사이킷런은 결정 트리 알고리즘이 학습을 통해 규칙을 정하는 데 있어 피처의 중요한 역할 지표를 feature_importances_ 속성으로 제공한다.
●feature_importances_ 값이 높을수록 해당 피처의 중요도가 높다
import seaborn as sns
import numpy as np
%matplotlib inline
# feature importance 추출
print('Feature importances:\n{0}'.format(np.round(dt_clf.feature_importances_, 3)))
# feature별 importance 매핑
for name, value in zip(iris_data.feature_names, dt_clf.feature_importances_):
print('{0}:{1:.3f}'.format(name, value))
# feature importance를 피처별로 시각화하기
sns.barplot(x=dt_clf.feature_importances_, y=iris_data.feature_names)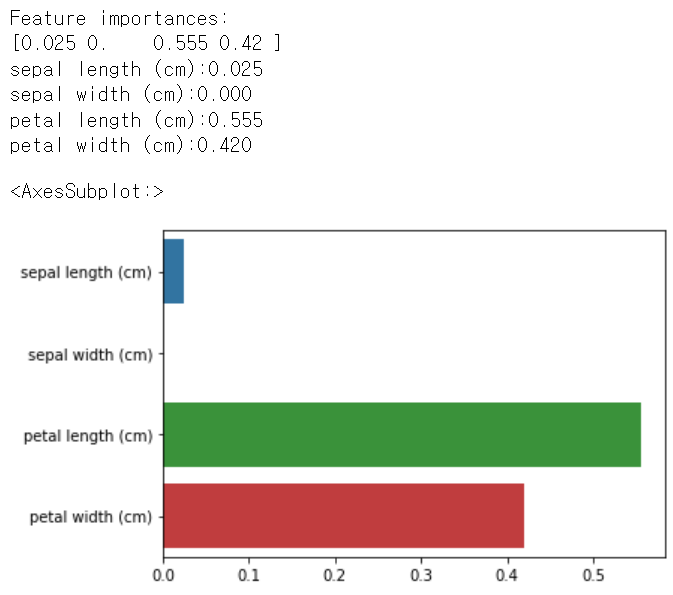
여러 피처들 중 petal length가 가장 피처 중요도가 높음을 알 수 있음
<결정 트리 과적합>
결정 트리가 어떻게 학습 데이터를 분할해 예측을 수행하는지와 이로 인한 과적합 문제를 구체적으로 알아보자!
사이킷런의 make_classification() 함수를 이용해 분류를 위한 임의의 데이터 세트를 만들고 이를 시각화한다.
;make_classification() 함수 참고 자료
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
%matplotlib inline
plt.title("3 Class values with 2 Features Sample data creation")
# 2차원 시각화를 위해서 feature는 2개, 결정값 클래스는 3가지 유형의 classification 샘플 데이터 생성.
X_features, y_labels = make_classification(n_features=2, n_redundant=0, n_informative=2,
n_classes=3, n_clusters_per_class=1,random_state=0)
# plot 형태로 2개의 feature로 2차원 좌표 시각화, 각 클래스값은 다른 색깔로 표시됨.
plt.scatter(X_features[:, 0], X_features[:, 1], marker='o', c=y_labels, s=25, cmap='rainbow', edgecolor='k')
이제 X_features와 y_labels 데이터 세트를 기반으로 결정 트리를 학습한다. 첫 번째 학습 시에는 결정 트리 생성에 별다른 제약이 없도록 결정 트리의 하이퍼 파라미터를 디폴트로 한 뒤, 결정 트리 모델이 어떠한 결정 기준을 가지고 분할하면서 데이터를 분류하는지 확인할 것이다. 이를 위해 별도의 함수 visualize_boundary()를 생성해 머신러닝 모델이 클래스 값을 예측하는 결정 기준을 색상과 경계로 나타내 모델이 어떻게 데이터 세트를 예측 분류하는지 본다.
import numpy as np
# Classifier의 Decision Boundary를 시각화 하는 함수
def visualize_boundary(model, X, y):
fig,ax = plt.subplots()
# 학습 데이터 scatter plot으로 나타내기
ax.scatter(X[:, 0], X[:, 1], c=y, s=25, cmap='rainbow', edgecolor='k',
clim=(y.min(), y.max()), zorder=3)
ax.axis('tight')
ax.axis('off')
xlim_start , xlim_end = ax.get_xlim()
ylim_start , ylim_end = ax.get_ylim()
# 호출 파라미터로 들어온 training 데이타로 model 학습 .
model.fit(X, y)
# meshgrid 형태인 모든 좌표값으로 예측 수행.
xx, yy = np.meshgrid(np.linspace(xlim_start,xlim_end, num=200),np.linspace(ylim_start,ylim_end, num=200))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# contourf() 를 이용하여 class boundary 를 visualization 수행.
n_classes = len(np.unique(y))
contours = ax.contourf(xx, yy, Z, alpha=0.3,
levels=np.arange(n_classes + 1) - 0.5,
cmap='rainbow', clim=(y.min(), y.max()),
zorder=1)from sklearn.tree import DecisionTreeClassifier
# 특정한 트리 생성 제약이 없도록 하이퍼 파라미터가 디폴트인 결정 트리의 학습과 결정 경계 시각화
dt_clf = DecisionTreeClassifier(random_state=156).fit(X_features, y_labels)
visualize_boundary(dt_clf, X_features, y_labels)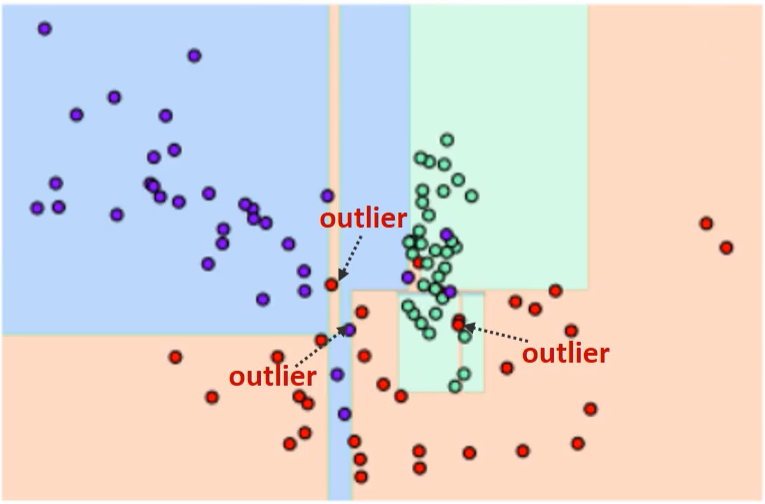
일부 이상치(outlier) 데이터까지 분류하기 위해 분할이 자주 일어나서 결정 기준 경계가 매우 많아졌다.
결정 트리의 기본 하이퍼 파라미터 설정은 리프 노드 안에 데이터가 모두 균일하거나 하나만 존재해야 하는 엄격한 분할 기준으로 인해 결정 기준 경계가 많아지고 복잡해졌다. 이렇게 복잡한 모델은 학습 데이터 세트의 특성과 약간만 다르 형태의 데이터 세트(테스트 데이터 세트)를 예측하면 예측 정확도가 떨어지는 과적합(overfitting)이 발생한다.
# min_samples_leaf=6으로 트리 생성 조건을 제약한 결정 경계 시각화
dt_clf = DecisionTreeClassifier(min_samples_leaf=6, random_state=156).fit(X_features, y_labels)
visualize_boundary(dt_clf, X_features, y_labels)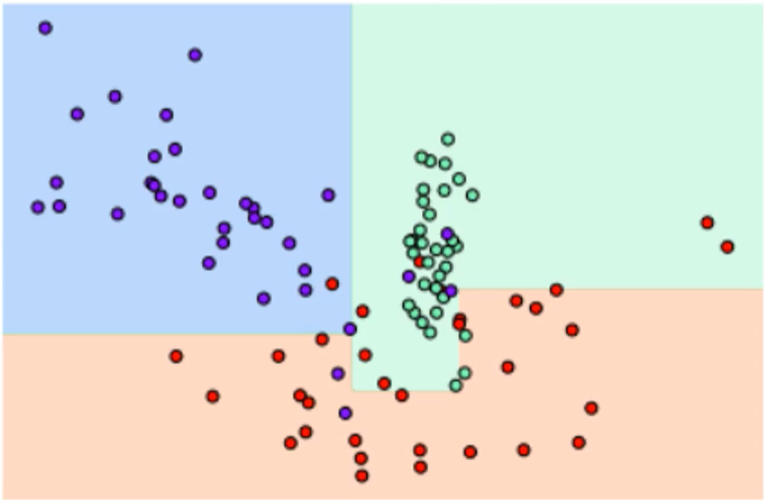
이상치에 크게 반응하지 않으면서 좀 더 일반화된 분류 규칙에 따라 분류됐음을 알 수 있다. 다양한 테스트 데이터 세트를 기반으로 한 결정 트리 모델의 예측 성능은 첫 번째 모델보다는 min_samples_leaf=6으로 트리 생성 조건을 제약한 모델이 더 뛰어날 가능성이 높다. 왜냐하면 테스트 데이터 세트는 학습 데이터 세트와는 다른 데이터 세트인데, 학습 데이터만 지나치게 최적화된 분류 기준은 오히려 테스트 데이터 세트에서 정확도를 떨어뜨릴 수 있는 과적합 문제 때문이다.
'파이썬 머신러닝 완벽가이드 > [4장] 분류' 카테고리의 다른 글
| 부스팅 (0) | 2023.02.10 |
|---|---|
| 배깅 (0) | 2023.02.09 |
| 앙상블 학습 (0) | 2023.02.09 |
| 결정 트리 실습 - 사용자 행동 인식 데이터 세트 (0) | 2023.02.09 |
| 분류(Classification)의 개요 (0) | 2023.02.04 |