하이퍼 파라미터 튜닝 수행 방법
대표적으로 GridSearch, RandomSearch, Bayesian Optimization, 수동 튜닝이 있다.
하이퍼 파라미터 튜닝의 주요 이슈
●Gradient Boosting 기반 알고리즘은 튜닝 해야 할 하이퍼 파라미터 개수가 많고 범위가 넓어서 가능한 개별 경우의 수가 너무 많음
●이러한 경우의 수가 많을 경우 데이터가 크면 하이퍼 파라미터 튜닝에 굉장히 오랜 시간이 투입되어야 함
GridSearch와 RandomSearch의 주요 이슈

GridSearch 방식으로 하이퍼 파라미터 튜닝을 한다면 5*4*6*6*4*4=11520회에 걸쳐서 반복적으로 학습과 평가를 수행해야만 하기에 수행 시간이 매우 오래 걸리고, 교차검증까지 같이 진행하면 cv 값 만큼 곱해져서 수행 시간이 매우 오래 걸림
●GridSearchCV는 수행 시간이 너무 오래 걸림. 개별 하이퍼 파라미터들은 Grid 형태로 지정하는 것은 한계가 존재(데이터 세트가 작을 때 유리)
●RandomizedSearch는 GridSearchCV를 랜덤하게 수행하면서 수행 시간은 줄여 주지만, Random한 선택으로 최적 하이퍼 파라미터 검출에 태생적 제약(데이터 세트가 클 때 유리)
●두 가지 방법 모두 iteration 중에 어느정도 최적화된 하이퍼 파라미터들을 활용하면서 최적화를 수행할 수 없음
Bayesian 최적화가 필요한 순간
●가능한 최소의 시도로 최적의 답을 찾아야 할 경우
●개별 시도가 너무 많은 시간/자원이 필요할 때
베이지안 최적화 개요
●베이지안 최적화는 알려지지 않은 목적 함수(블랙 박스 형태의 함수)에서, 최대 또는 최소의 함수 반환값을 만드는 최적해(최적 입력값)를 짧은 반복을 통해 찾아내는 방식
●베이지안 확률에 기반을 두고 있는 최적화 기법
- 베이지안 확률이 새로운 데이터를 기반으로 사후 확률을 개선해 나가듯이, 베이지안 최적화는 새로운 데이터를 입력받았을 때 최적 함수를 예측하는 사후 모델을 개선해 나가면서 최적 함수 모델을 만들어 낸다.
●베이지안 최적화의 주요 요소
1. 대체 모델(Surrogate Model)
2. 획득 함수(Acquisition Function)
대체 모델은 획득 함수로부터 최적 함수를 예측할 수 있는 입력값을 추천 받은 뒤 이를 기반으로 최적 함수 모델을 개선해 나가며, 획득 함수는 개선된 대체 모델을 기반으로 최적 입력값을 계산하는 방식
이때 입력값은 하이퍼 파라미터이다. 즉, 대체 모델은 획득 함수가 계산한 하이퍼 파라미터를 입력받으면서 점차적으로 모델 개선을 수행, 획득 함수는 개선된 대체 모델을 기반으로 더 정확한 하이퍼 파라미터를 계산
베이지안 최적화 프로세스
1) 최초에는 랜덤하게 하이퍼 파라미터들을 샘플링하고 성능 결과를 관측
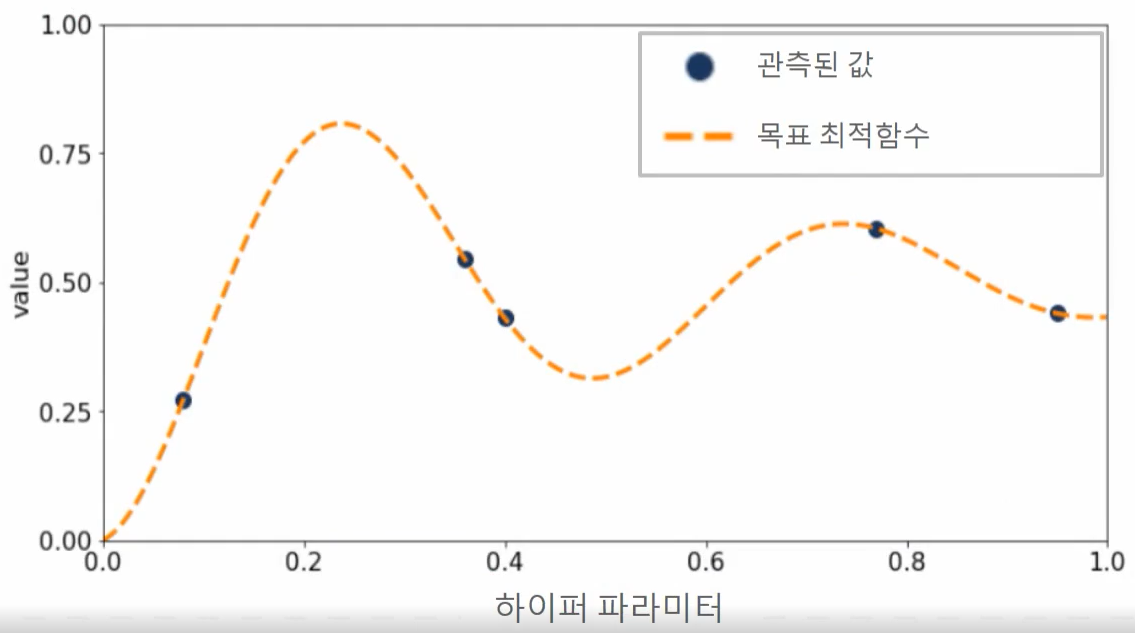
검은색 원은 특정 하이퍼 파라미터가 입력되었을 때 관측된 성능 지표 결과값을 뜻하며 주황색 사선은 찾아야 할 목표 최적함수 이다.
2) 관측된 값을 기반으로 대체 모델은 최적 함수를 추정
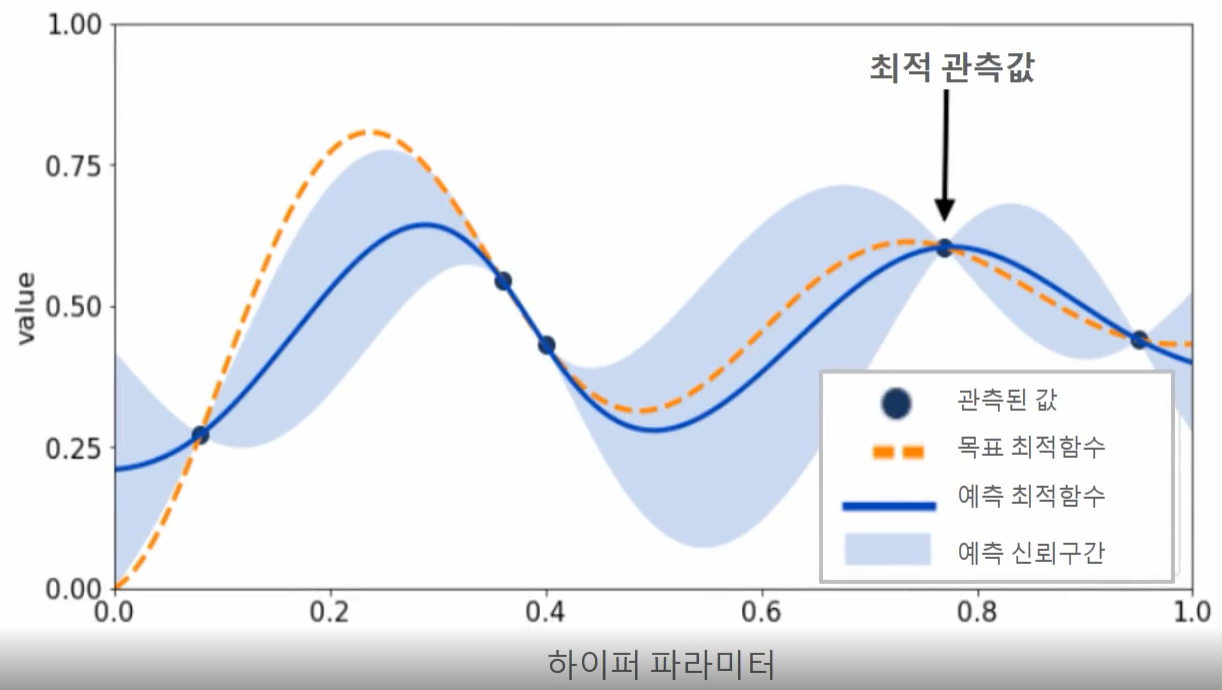
파란색 실선은 대체 모델이 추정한 최적 함수이다. 하늘색 영역은 예측된 예측된 함수의 신뢰 구간으로, 추정된 함수의 결과값 오류 편차를 의미하며 추정 함수의 불확실성을 나타낸다.
최적 관측값은 y축 value에서 가장 높은 값을 가질 때의 하이퍼 파라미터이다.
3) 추정된 최적 함수를 기반으로 획득 함수에서 다음으로 관측할 하이퍼 파라미터 추천

획득 함수는 이전의 최적 관측값보다 더 큰 최대값을 가질 가능성이 높은 지점을 찾아서 다음에 관측할 하이퍼 파라미터를 대체 모델에 전달한다.
4) 획득 함수로부터 전달된 하이퍼 파라미터로 관측된 값을 기반으로 대체 모델은 갱신되어 다시 최적 함수 예측 추정
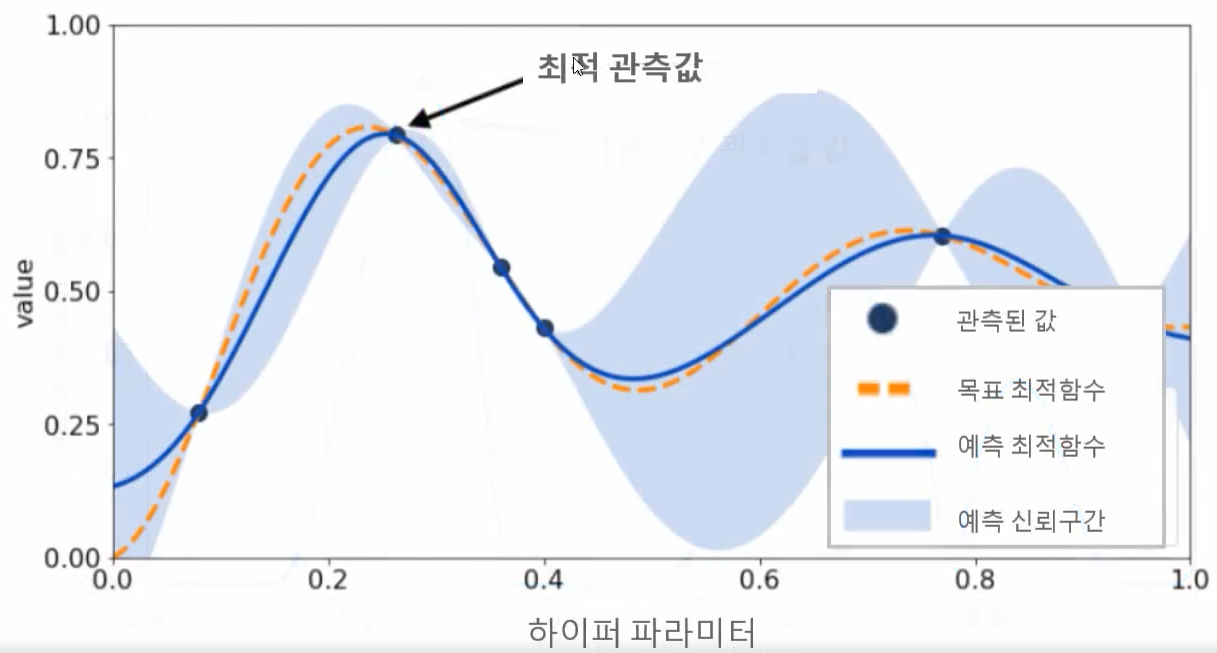
이런 방식으로 3번과 4번 과정을 특정 횟수만큼 반복하게 되면 대체 모델의 불확실성이 개선되고 점차 정확한 최적 함수 추정이 가능해진다.
HyperOpt 사용법
대체 모델은 최적 함수를 추정할 때 다양한 알고리즘을 사용할 수 있다. 일반적으로는 가우시안 프로세스(Gaussian Process)를 적용하지만, HyperOpt는 트리 파르젠 Estimator(TPE, Tree-structure Parzen Estimator)를 사용한다.
HyperOpt는 다음과 같은 로직을 통해 사용할 수 있다.
1. 입력 변수명과 입력값의 검색 공간(Search Space) 설정
2. 목적 함수 설정
3. fmin() 함수를 통해 베이지안 최적화 기법에 기반한 목적 함수의 반환값이 최솟값을 가지는 최적 입력값 유추
설치
!pip install hyperopt검색 공간 설정
# hp 모듈은 입력값의 검색 공간을 다양하게 설정할 수 있도록 여러 함수를 제공
- hp.quniform(label, low, high, q): label로 지정된 입력 변수명 검색 공간을 최솟값 low에서 최대값 high까지 q의 간격을 가지고 설정
- hp.uniform(label, low, high): 최솟값 low에서 최대값 high까지 정규 분포 형태의 검색 공간 설정
- hp.randint(label, upper): 0부터 최대값 upper까지 random한 정수값으로 검색 공간 설정
- hp.loguniform(label, low, high): exp(uniform(low, high)값을 반환하며, 반환 값의 log 변환된 값은 정규 분포 형태를 가지는 검색 공간 설정
- hp.choice(label, options): 검색 값이 문자열 또는 문자열과 숫자값이 섞여 있을 경우 설정. options는 리스트나 튜플 형태로 제공되며 hp.choice('tree_criterion', ['gini', 'entropy'])와 같이 설정하면 입력 변수 tree_criterion의 값을 'gini'와 'entropy'로 설정하여 입력함
from hyperopt import hp
# -10 ~ 10까지 1간격을 가지는 입력 변수 x, -15 ~ 15까지 1간격을 가지는 입력 변수 y 설정
search_space = {'x':hp.quniform('x', -10, 10, 1), 'y':hp.quniform('y', -15, 15, 1)}목적 함수 생성
from hyperopt import STATUS_OK
# 목적 함수를 생성. 변수값과 변수 검색 공간을 가지는 딕셔너리를 인자로 받고, 특정값을 반환
def objective_func(search_space):
x = search_space['x']
y = search_spaec['y']
retval = x**2 -20*y # retval = x**2-20*y로 계산된 값을 반환하게 설정한 이유는 예제를 위해서 임의로 만든것
return retval
# hyperopt에서 목적 함수의 반환값은 권장하는 양식이 다음과 같음
# return {'loss':retval, 'status':STATUS_OK}
# return retval 만 해도 잘 반환됨fmin() 함수를 통해 베이지안 최적화 기법에 기반한 목적 함수의 반환값이 최솟값을 가지는 최적 입력값 유추
# fmin() 함수의 주요 인자
- fn: 위에서 생성한 objective_func와 같은 목적 함수
- space: 위에서 생성한 search_space와 같은 검색 공간
- algo: 베이지안 최적화 적용 알고리즘. 기본적으로 tpe.suggest이며 이는 HyperOpt의 기본 최적화 알고리즘인 TPE(Tree of Parzen Estimator)를 의미
- max_evals: 최적 입력값을 찾기 위한 입력값 시도 횟수
- trials: 최적 입력값을 찾기 위해 시도한 입력값 및 해당 입력값의 목적 함수 반환값 결과를 저장하는데 사용. Trials 클래스를 객체로 생성한 변수명을 입력함
- rstate: fmin()을 수행할 때마다 동일한 결과값을 가질 수 있도록 설정하는 랜덤 시드 값
rstate는 예제 결과와 동일하게 만들기 위해 적용했으며, 경험적으로 적용 안하는 것이 더 좋은 결과를 반환한 경우가 많았음→일반적으로 rstate를 잘 적용하지 않음
HyperOpt는 rstate에 넣어주는 인자값으로 일반적인 정수형 값을 넣지 않는다. 또한 버전별로 rstate 인자값이 조금씩 다르다. 현 버전인 0.2.7에서는 넘파이의 random Generator를 생성하는 random.default_rng() 함수 인자로 seed값을 입력하는 방식
from hyperopt import fmin, tpe, Trials
import numpy as np
# 입력값 및 해당 입력값의 목적 함수 반환값 결과를 저장할 Trials 객체값 생성
trial_val = Trials()
# 목적 함수의 반환값이 최솟값을 가지는 최적 입력값을 5번의 입력값 시도(max_evals=5)로 찾아냄
best_01 = fmin(fn=objective_func, space=search_space, algo=tpe.suggest, max_evals=5,
trials=trial_val, rstate=np.random.default_rng(seed=0))
print('best:', best_01)
입력 변수 x의 공간 -10 ~ 10, y의 공간 -15 ~ 15에서 목적 함수의 반환값을 x**2 -20*y로 설정했으므로 x는 0에 가까울수록 y는 15에 가까울수록 반환값이 최소로 근사될 수 있다. 확실하게 만족할 수준의 최적 x와 y값을 찾은 것은 아니지만, 5번의 수행으로 어느 정도 최적값에 다가설 수 있었다는 점은 주지할만하다.
trial_val = Trials()
# max_evals를 20회로 늘려서 재테스트
best_02 = fmin(fn=objective_func, space=search_space, algo=tpe.suggest, max_evals=20,
trials=trial_val, rstate=np.random.default_rng(seed=0))
print('best:', best_02)
max_evals=20으로 재테스트 시 x는 2, y는 15로 만족할 수준의 최적 x와 y값을 찾음
만일 그리드 서치와 같이 순차적으로 x, y 변수값을 입력해서 최소 함수 반환값을 찾는다면, 입력값 x는 -10 ~ 10까지 21개의 경우의 수, 입력값 y는 -15 ~ 15까지 31개의 경우의 수로 21*31=651회의 반복이 필요한데, 베이지안 최적화를 이용해서 는 20회의 반복만으로 일정 수준의 최적값을 근사해 낼 수 있다.
→베이지안 최적화 방식은 상대적으로 최적값을 찾는 시간을 많이 줄여 줌
Trials 객체 더 알아보기
Trials 객체의 중요 속성
- results: 함수의 반복 수행 시마다 반환되는 반환값
- vals: 함수의 반복 수행 시마다 입력되는 입력 변수값
# result: 리스트 내부의 개별 원소는 {'loss':함수 반환값, 'status':반환 상태값}와 같은 딕셔너리
print(trial_val.results)
# vals: {'입력변수명':개별 수행 시마다 입력된 값의 리스트}와 같은 형태
print(trial_val.vals)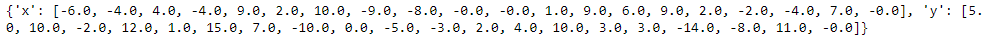
Trials 객체의 result와 vals 속성은 HyperOpt의 fmin() 함수의 수행 시마다 최적화되는 경과를 볼 수 있는 함수 반환값과 입력 변수값들의 정보를 제공
가독성을 높이기 위해 DataFrame으로 만들어서 확인해보자!
import pandas as pd
# result에서 loss 키값에 해당하는 value를 추출하여 list로 생성
losses = [loss_dict['loss'] for loss_dict in trial_val.results]
# DataFrame으로 생성
result_df = pd.DataFrame({'x':trial_val.vals['x'], 'y':trial_val.vals['y'], 'losses':losses})
result_df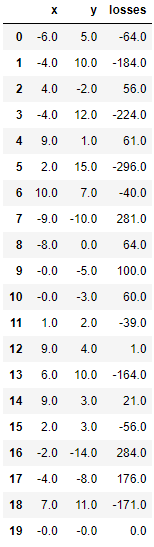
'파이썬 머신러닝 완벽가이드 > [4장] 분류' 카테고리의 다른 글
| 캐글 산탄데르 고객 만족 예측 (0) | 2023.02.23 |
|---|---|
| 베이지안 최적화 기반의 HyperOpt를 이용한 하이퍼 파라미터 튜닝(2) (0) | 2023.02.22 |
| LightGBM (0) | 2023.02.19 |
| 부스팅 정리 (0) | 2023.02.15 |
| XGBoost(eXtra Gradient Boost) (2) (0) | 2023.02.14 |